Errori di tipo I e di tipo II nei test A/B e come evitarli

Il test A/B comporta la suddivisione casuale del traffico in entrata sul tuo sito Web tra più varianti di una particolare pagina Web per valutare quale influisca positivamente sulle tue metriche critiche. Abbastanza semplice, giusto? Beh, non così tanto. Mentre il test A/B può sembrare semplice, la scienza e la matematica dietro il suo funzionamento e il calcolo dei risultati possono diventare piuttosto complicati.

La statistica è la pietra angolare dei test A/B e il calcolo delle probabilità è la base delle statistiche. Pertanto, non puoi mai essere sicuro al 100% dell'accuratezza dei risultati che ricevi o ridurre il rischio allo 0%. Invece, puoi solo aumentare la possibilità che il risultato del test sia vero. Ma come proprietari di test, non dovresti preoccuparti di questo poiché il tuo strumento dovrebbe occuparsene.

Anche dopo aver seguito tutti i passaggi essenziali, i rapporti sui risultati dei test potrebbero essere distorti da errori che si insinuano inconsapevolmente nel processo. Popolarmente noti come errori di Tipo I e Tipo II, questi portano essenzialmente a una conclusione errata dei test e/o alla dichiarazione errata di vincitore e perdente. Ciò causa un'errata interpretazione dei rapporti sui risultati dei test, che alla fine fuorvia l'intero programma di ottimizzazione e potrebbe costarti conversioni e persino entrate.

Diamo un'occhiata più da vicino a cosa intendiamo esattamente per errori di tipo I e di tipo II, le loro conseguenze e come evitarli.

Quali sono alcuni degli errori che si insinuano nei risultati del test A/B?

Errori di tipo I

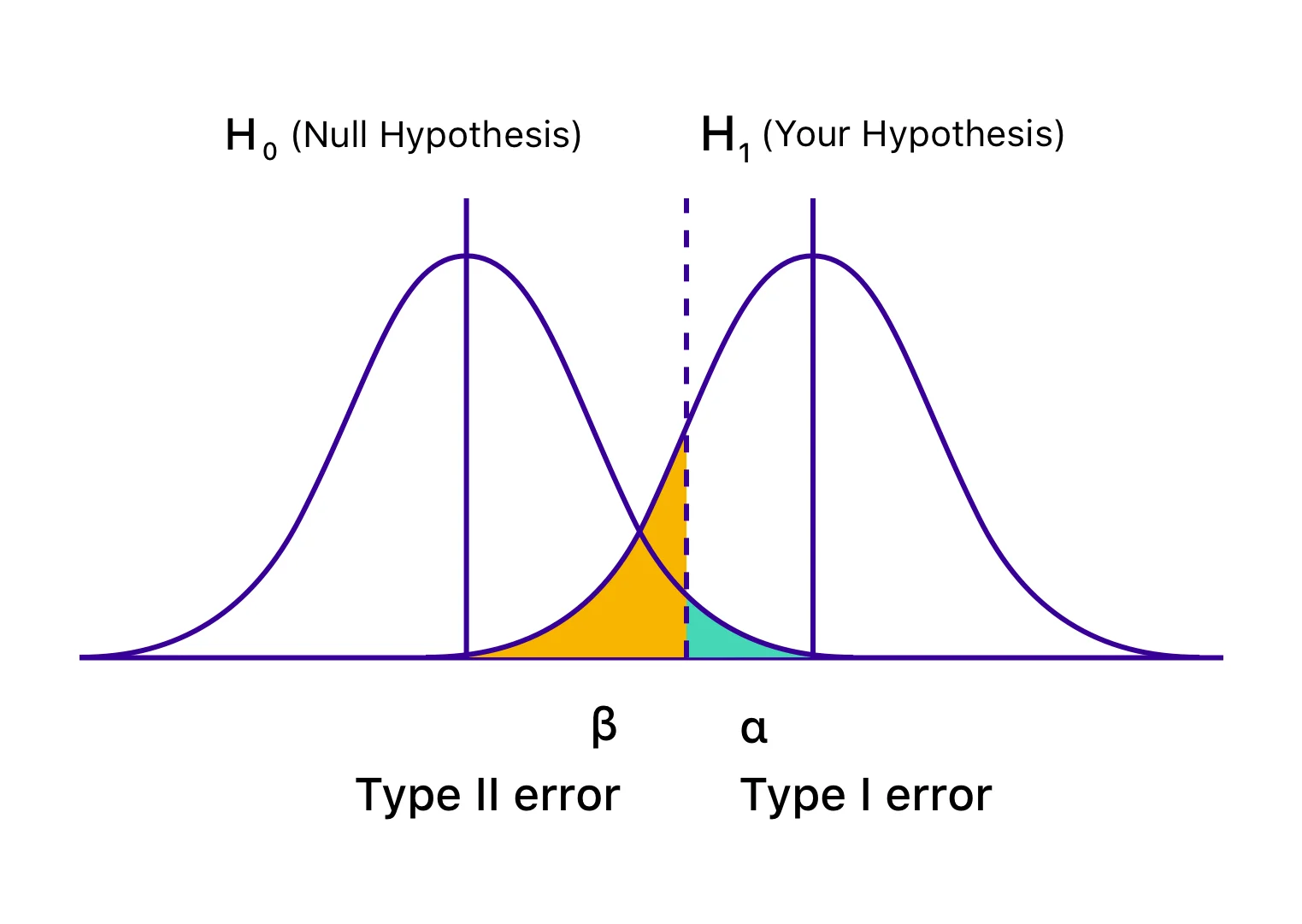
Conosciuti anche come errori alfa (α) o falsi positivi, nel caso dell'errore di tipo I, il tuo test sembra avere esito positivo e la tua variazione sembra causare un impatto (migliore o peggiore) sugli obiettivi definiti per il test. Tuttavia, l'aumento o il calo è, in effetti, solo temporaneo e non durerà una volta distribuita la versione vincente universalmente e misurato il suo impatto per un periodo significativo. Succede quando concludi il tuo test prima di raggiungere la significatività statistica o i criteri prestabiliti e ti precipiti a rifiutare la tua ipotesi nulla e ad accettare la variazione vincente. L'ipotesi nulla afferma che la suddetta modifica non avrà alcun impatto sulla metrica/obiettivo data. E nel caso degli errori di tipo I, l'ipotesi nulla è vera ma respinta a causa della conclusione prematura dei test o dell'errore di calcolo dei criteri per la conclusione.

La probabilità di commettere un errore di tipo I è indicata da 'α' e correlata al livello di confidenza, in cui si decide di concludere il test. Ciò significa che se concludi il test a un livello di confidenza del 95%, accetti che ci sia una probabilità del 5% di ottenere il risultato sbagliato. Allo stesso modo, se il livello di confidenza è del 99%, la probabilità che il risultato del test sia errato è dell'1%. Potresti chiamarla pura sfortuna, ma se ti imbatti in un errore α anche dopo aver concluso il test a un livello di confidenza del 95%, significa che si è verificato un evento con solo il 5% di probabilità.

Supponiamo che tu elabori un'ipotesi secondo cui spostare la CTA della tua pagina di destinazione su above the fold comporterà un aumento del numero di iscrizioni. L'ipotesi nulla qui è che non ci sarebbe alcun impatto sulla modifica del posizionamento del CTA sul numero di iscrizioni ricevute. Una volta iniziato il test, sei tentato di dare un'occhiata ai risultati e notare un enorme aumento del 45% delle iscrizioni generato dalla variazione entro una settimana. Sei convinto che il contrasto sia notevolmente migliore e finisci per concludere il test, rifiutando l'ipotesi nulla e implementando la variazione universalmente, solo per notare che non ha più un impatto simile ma invece non ha alcun impatto. L'unica spiegazione è che il rapporto sui risultati del test è stato distorto dall'errore di tipo I.

Come evitare errori di tipo I

Anche se non puoi eliminare completamente la possibilità di incappare in un errore di tipo I, puoi sicuramente ridurlo. Per questo, assicurati di concludere i tuoi test solo quando hanno raggiunto un livello di confidenza sufficientemente alto. Un livello di confidenza del 95% è considerato l'ideale ed è ciò che devi mirare a raggiungere. Anche dopo aver raggiunto un livello di confidenza del 95%, i risultati del test potrebbero essere alterati dall'errore di tipo I (come discusso sopra). Pertanto, devi anche assicurarti di eseguire i test per un periodo sufficientemente lungo da garantire che sia stata testata una buona dimensione del campione, aumentando così la credibilità dei risultati dei test.

Puoi utilizzare il calcolatore della durata del test A/B di VWO per determinare il periodo ideale per il quale devi eseguire un test particolare. Allo stesso modo, puoi anche calcolare la dimensione del campione del tuo test A/B per assicurarti di concludere i test solo quando hai la minima possibilità di finire con risultati adulterati.

Il motore di statistiche basato su modello bayesiano di VWO, SmartStats, ti aiuta a ridurre la probabilità di incontrare un errore di tipo 1.

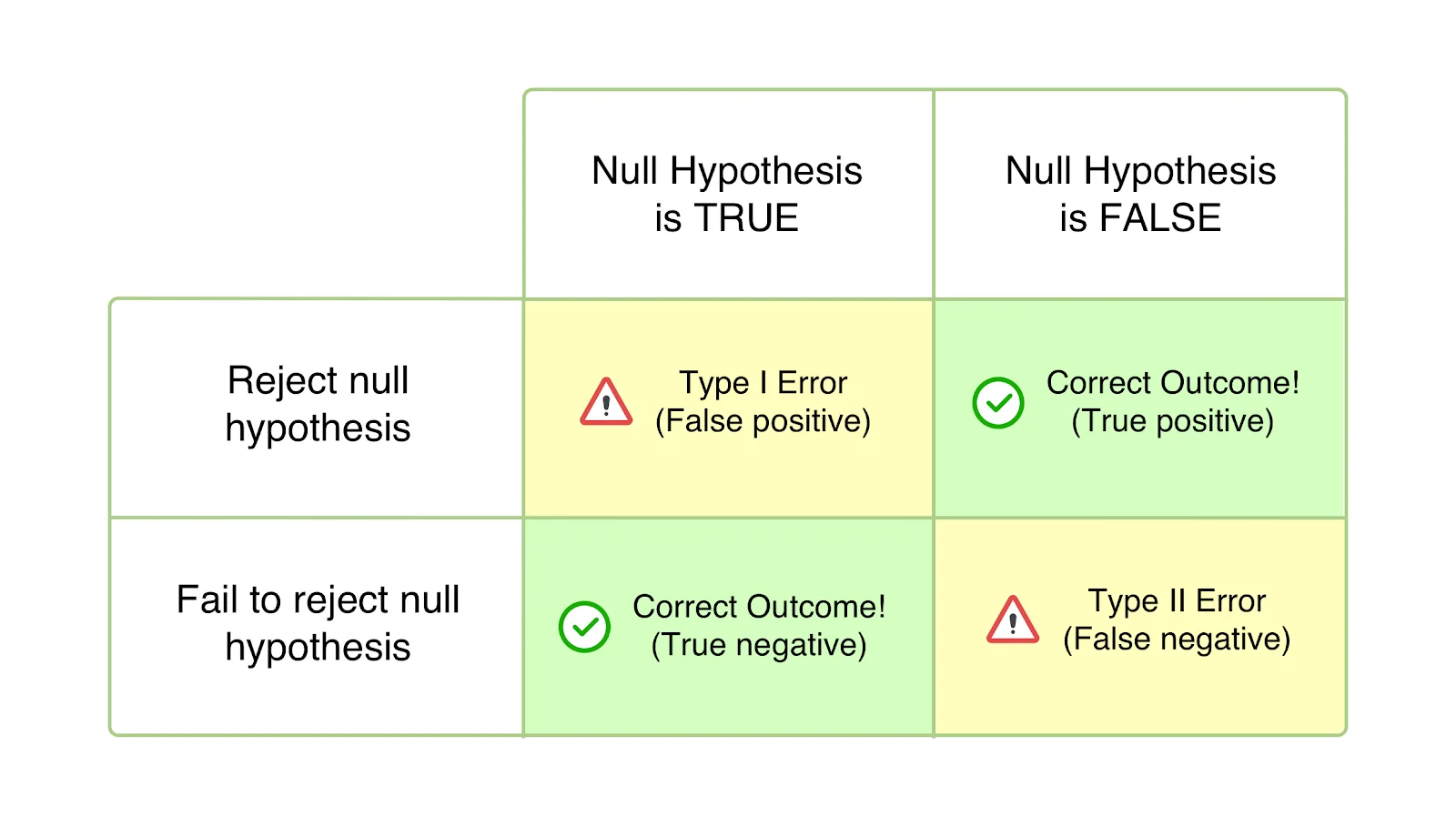
Errori di tipo II

Conosciuti anche come errori Beta (β) o falsi negativi, nel caso di errori di tipo II, un test particolare sembra essere inconcludente o non riuscito, con l'ipotesi nulla che sembra essere vera. In realtà, la variazione ha un impatto sull'obiettivo desiderato, ma i risultati non vengono mostrati e l'evidenza favorisce l'ipotesi nulla. Pertanto, finisci per (erroneamente) accettare l'ipotesi nulla e rifiutare la tua ipotesi e variazione.

Gli errori di tipo II di solito portano all'abbandono e allo scoraggiamento dei test ma, nei casi peggiori, alla mancanza di motivazione a perseguire la tabella di marcia CRO poiché si tende a ignorare gli sforzi, presumendo che non abbiano avuto alcun impatto.

'β' indica la probabilità di commettere un errore di tipo II. La probabilità di non incorrere in un errore di tipo II è indicata da 1 – β, dipendente dalla potenza statistica del test. Maggiore è la potenza statistica del test, minore è la probabilità di incontrare un errore di tipo II. Se stai eseguendo un test con una potenza statistica del 90%, c'è solo una probabilità del 10% che potresti finire con un falso negativo.

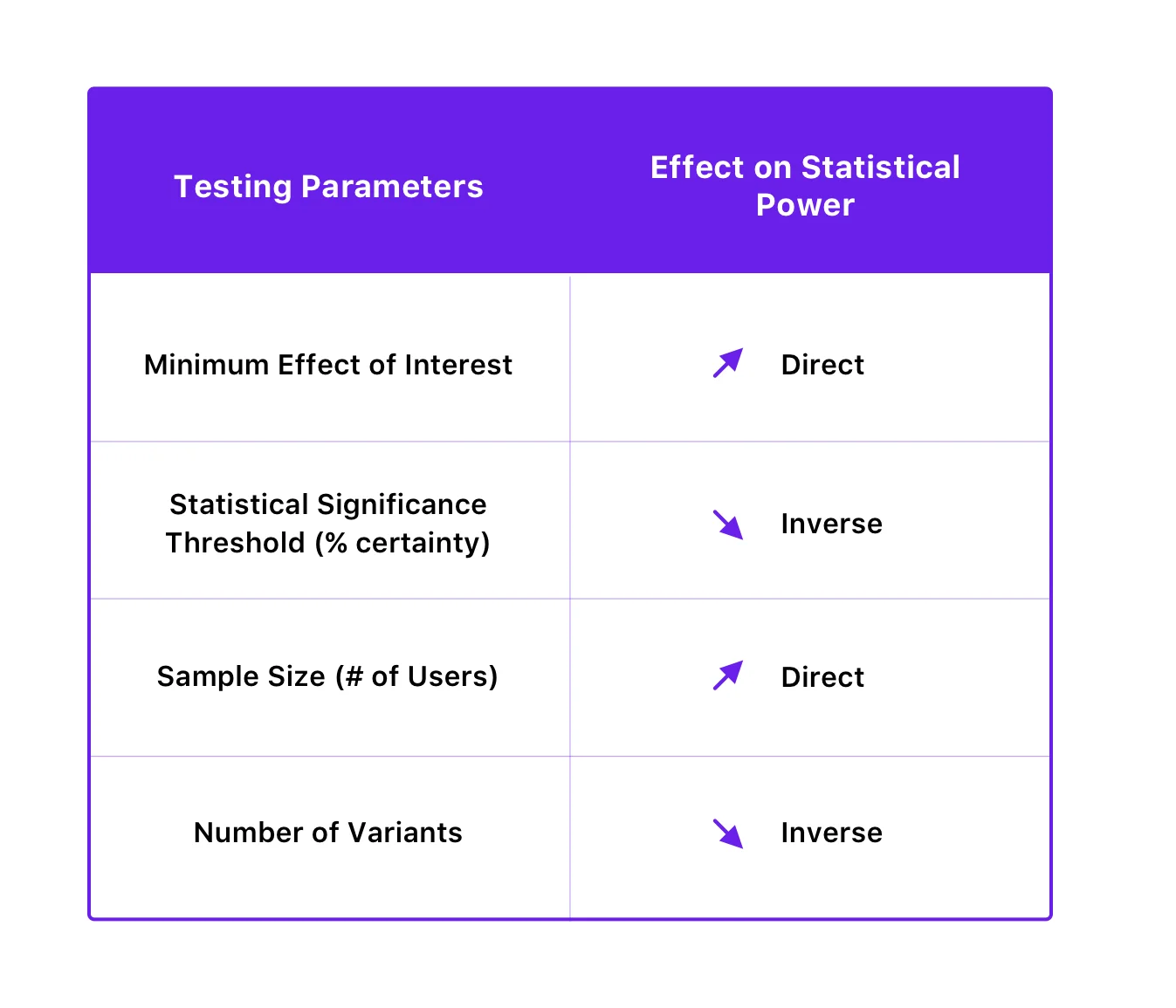
La potenza statistica di un test dipende dalla soglia di significatività statistica, dalla dimensione del campione, dalla dimensione minima dell'effetto di interesse e persino dal numero di variazioni del test.

Ecco come sono correlati:

Supponiamo che tu ipotizzi che l'aggiunta di badge di sicurezza sulla tua pagina di pagamento ti aiuterebbe a ridurre la percentuale di abbandono in quella fase. Crei una variante della pagina di pagamento con i badge di sicurezza ed esegui il test, solo per dare un'occhiata ai risultati 10 giorni dopo il suo inizio. Non avendo notato alcuna variazione nel numero di conversioni o drop-off, decidi di concludere il test e di dichiarare vera l'ipotesi nulla. Non convinto dai risultati del test, decidi di eseguire nuovamente il test, solo che questa volta lo lasci funzionare più a lungo. Di conseguenza, questa volta noti un miglioramento significativo del tuo obiettivo di conversione. Quello che è successo la prima volta è che hai riscontrato l'errore di tipo II concludendo il test prima del tempo richiesto.

Come evitare errori di tipo II

Migliorando la potenza statistica dei tuoi test, puoi evitare errori di tipo II. Puoi farlo aumentando la dimensione del campione e diminuendo il numero di varianti. È interessante notare che il miglioramento della potenza statistica per ridurre la probabilità di errori di tipo II può essere ottenuto anche diminuendo la soglia di significatività statistica, ma, a sua volta, aumenta la probabilità di errori di tipo I. Tuttavia, poiché ridurre la probabilità di errori di tipo I di solito ha la precedenza sull'evitare errori di tipo II (poiché le sue conseguenze possono essere più gravi), è consigliabile non interferire con la soglia di significatività statistica al fine di migliorare la potenza.

VWO SmartStats: il modo bayesiano più intelligente per il processo decisionale aziendale

Idealmente, come proprietario di un test, le statistiche non sono qualcosa su cui dovresti concentrarti poiché la tua ricerca non è trovare la verità con i tuoi esperimenti: il tuo motivo è prendere una decisione aziendale migliore che generi maggiori entrate per te. Quindi, l'importante è lavorare con uno strumento che ti aiuti a fare una scelta migliore e più intelligente, senza che tu debba entrare nei dettagli delle statistiche.

Secondo il modello frequentista della statistica inferenziale, la conclusione di un test dipende interamente dal raggiungimento della significatività statistica. Se si termina un test prima che raggiunga la significatività statistica, è probabile che si finisca con un falso positivo (errore di tipo I).

Il motore di statistiche basato su modello bayesiano di VWO, SmartStats, calcola la probabilità che questa variazione superi il controllo, nonché la potenziale perdita che potresti subire durante l'implementazione. VWO ti mostra la possibile perdita associata all'implementazione della variazione in modo da poter fare una scelta informata.

Questa potenziale perdita aiuta anche a decidere quando concludere un particolare test. Dopo la conclusione della prova, la variazione è dichiarata vincitrice solo se la potenziale perdita della variazione è inferiore ad una certa soglia. Questa soglia è determinata tenendo conto del tasso di conversione della versione di controllo, del numero di visitatori che hanno partecipato al test e di un valore costante.

VWO SmartStats non solo riduce i tempi di test del 50%, poiché non ti affidi al raggiungimento di un tempo prestabilito e della dimensione del campione per concludere il test, ma ti dà anche un maggiore controllo sui tuoi esperimenti. Ti dà una chiara probabilità che ti aiuta a prendere decisioni in base al tipo di test che stai eseguendo. Ad esempio, se stai testando una modifica a basso impatto come la modifica del colore del pulsante, forse una probabilità del 90% è sufficiente per definire vincente una variazione. Oppure, se stai testando qualcosa nell'ultimo passaggio della canalizzazione, potresti voler aspettare fino al 99% di probabilità. Sei, quindi, nella posizione di aumentare la velocità dei test concludendo più rapidamente i test a basso impatto e dando priorità a quelli ad alto impatto nella tua tabella di marcia.

Un modello statistico basato su frequentisti ti darà solo la probabilità di vedere una differenza nelle variazioni supponendo che si tratti di un test A/A. Questo approccio, tuttavia, presuppone che si stia eseguendo il calcolo del test solo dopo aver ottenuto una dimensione campionaria sufficiente. VWO SmartStats non fa ipotesi, ma ti consente di prendere decisioni aziendali più intelligenti riducendo la probabilità di incappare in errori di Tipo I e Tipo II. Questo perché stima la probabilità che la variazione batta il controllo, di quanto, insieme alla perdita potenziale associata associata, consentendo di monitorare continuamente queste metriche durante l'esecuzione del test.

Poiché puntare alla certezza assoluta è estremamente difficile con le statistiche, non è possibile eliminare la possibilità che i risultati del test non vengano distorti a causa di un errore. Tuttavia, scegliendo uno strumento robusto come VWO, puoi ridurre le tue possibilità di commettere errori o ridurre il rischio associato a questi errori a un livello accettabile. Per saperne di più su come esattamente VWO può impedirti di cadere preda di tali errori, prova la versione di prova gratuita di VWO o richiedi una demo da uno dei nostri esperti di ottimizzazione.