使用直方图进行密度估计

概率密度函数 (PDF) 描述了在某个空间区域中观察到某个连续随机变量的概率。 对于一维随机变量 X，回想一下 PDF f(x) 遵循以下属性：

变量取值之间的概率

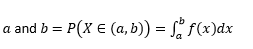
变量取值完全等于的概率

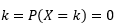
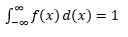
从观察样本中估计这样的 PDF 是机器学习中的常见问题。 这在许多异常值检测算法中很方便，我们试图根据样本观察估计“真实”分布，然后将一些现有或新的观察结果分类为异常值或非异常值。 例如，对发现欺诈感兴趣的汽车保险公司可能会检查每种类型的车身（例如保险杠更换）的索赔金额请求，并将任何过高的金额标记为潜在欺诈。 作为另一个例子，儿童心理学家可以检查不同儿童完成给定任务所花费的时间，并标记那些花费太长或太短时间进行潜在调查的儿童。

在这篇博客文章中，我们讨论了如何从观察样本中学习 PDF ，以便我们可以计算每个观察的概率并确定它是常见的还是罕见的。

使用直方图进行密度估计

首先，我们生成一些随机数据进行演示。

set.seed(123)
data <- c(rnorm(200, 10, 20), rnorm(200, 60, 30), runif(200, 120, 180)) # 600 points

接下来，我们使用直方图将它们可视化以供我们理解，如图 1 所示。

# Plot 1
hist(data, breaks=50, freq=F, main="Univariate Distribution", xlab="Data Value")
# Plot 2
hist(data, breaks=20, freq=F, main="", xlab="20 Data Bins", col='red', border='red')
par(new=T)
hist(data, breaks=100, freq=F, main="Univariate Distribution", xlab=NULL, xaxt='n', yaxt='n')

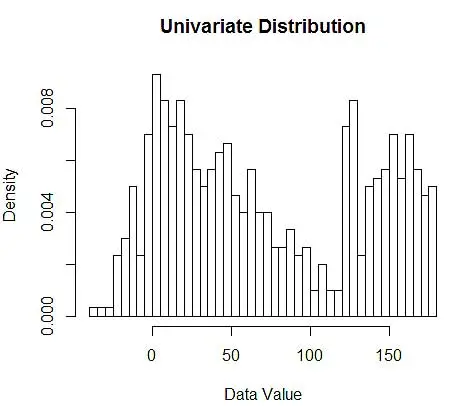
虽然直方图是数据可视化的图表，但您也可以看到它们是我们对密度的第一次估计。 更具体地说，我们可以通过将数据划分为 bin 来估计密度，并假设密度在该 bin 范围内是恒定的，并且其值等于落入该 bin 的观察数占观察总数的比例

因此，估计的 PDF 为

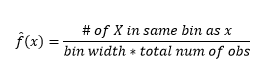
并且您意识到您已经对 bin-width 做出了假设，这将影响密度估计。 因此bin-width 是使用 histogram 的密度估计模型的参数。 然而，被忽略的事实是，我们还使用了另外一个参数——即第一个 bin 的起始位置。 您可以看到这可能如何影响所有箱的密度估计。 为了查看 bin-width 的影响，图 2 将密度估计与 20-bin 和 100-bin 直方图重​​叠。 查看环绕区域，其中较少/较粗的 bin 给出平坦的密度估计，而许多/较细的 bin 给出不同的密度估计。 对于黄点，来自两个不同模型的密度估计值将在 0.004 到 0.008 之间。

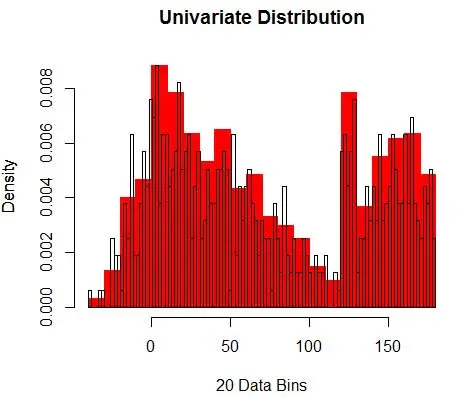
因此，正确选择参数对于获得正确的密度估计至关重要。 我们会解决这个问题，但请注意，直方图还存在其他问题。 使用直方图的密度估计非常不稳定和不连续。 一个 bin 的密度是平坦的，然后在 bin 外无限小的点突然急剧变化。 这使得错误估计的后果对于实际问题更加严重。

最后，为了便于说明，我们一直在使用单维变量，但实际上大多数问题都是多维的。 由于箱的数量随着维度的数量呈指数增长，估计密度所需的观察数量也会增长。 事实上，尽管有数百万个观测值，但许多箱仍然是空的或包含个位数的观测值，这似乎是合理的。 每个只有 3 个维度的 50 个 bin，我们有 503=125000 个需要填充的单元。 假设均匀分布，每个单元平均有 8 次观察，一百万个观察训练数据。

如何选择合适的参数？

对于 bin 宽度 n 的观察次数 N 对于 bin J 的观察比例是

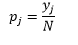
和密度估计是

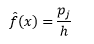
统计理论证明，虽然 f(x) 是 bin 中密度的期望值，但密度的方差是

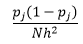
虽然我们可以通过减小 bin-width n 来获得更好的密度估计，但我们会增加估计的方差，因为我们可以直观地感觉到 bin-width 太细。 我们可以使用留一法交叉验证技术来估计最优参数集。 我们可以使用除一个之外的所有观测值来估计密度，然后计算遗漏观测值的密度并测量估计误差。 对直方图进行数学求解，为给定 bin 宽度的损失函数提供了一个封闭形式的解决方案。

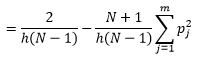
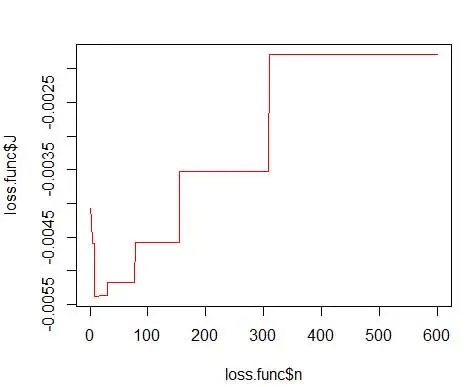
其中 m 是箱数。 上述技术细节在本讲座 [pdf] 中。 我们可以针对不同数量的 bin 绘制此损失函数（图 3）

getLoss <- function(n.break) {
N <- 600
res <- hist(data, breaks=n.break, freq=F)
bin <- as.numeric(res$breaks)
h <- bin[2]-bin[1]
p <- res$density
p <- p * h
return ( 2/(h*(N-1)) - ( (N+1)/(h*(N-1))*sum(p*p) ) )
}
loss.func <- data.frame(n=1:600)
loss.func$J <- sapply(loss.func$n, function(x) getLoss(x))
# Plot 3
plot(loss.func$n, loss.func$J, col='red', type='l')
opt.break <- max(loss.func[loss.func$J == min(loss.func$J), 'n'])
print(opt.break)
# Plot 4
hist(data, breaks=opt.break, freq=F, main="Univariate Distribution", xlab="15 Data Bins")

并获得最佳数字为 15。实际上 8-15 之间的任何值都可以。

因此，图 4 下面是密度估计，它平衡了密度值和粒度（具有最佳偏差-方差权衡）。

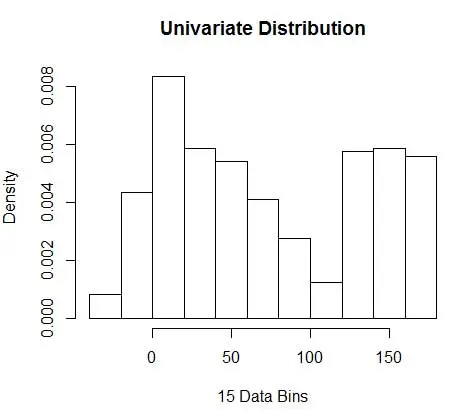
如果你在这一点上感到有点不安，那么我和你在一起。 尽管 bin 的数量在数学上是最优的，但感觉估计太粗略了。 没有直观的感觉为什么我们做得最好。 并且不要忘记关于起始位置、不连续估计和维度灾难的其他问题。 不要失望，有更好的方法。 在下一篇文章中，我们将讨论使用内核进行密度估计。